PCM and DPCM using SIMULINK
- AIM:
To generate a Pulse Code Modulation using simulink.
- SOFTWARE REQUIRED:
1.Matlab
2.Simulink
- BLOCKS REQUIRED:
1. Sine wave generator
2. Pulse generator
3. Product
4. Quantizer
5. Encoder
6. Integer to bit converter
7. Scope
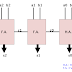
- BLOCK DIAGRAM for PCM:
- OUTPUTS OBTAINED:
quantized output
encoded output
PCM
- BLOCK DIAGRAM FOR DPCM:
- OUTPUTS OBTAINED:
after introducing a delay element
quantization
encoded signal
- INFERENCE
Pulse Time Modulation is also known as Pulse Width Modulation or Pulse Length Modulation. In PWM, the
samples of the message signal are used to vary the duration of the individual pulses. Width may be varied by
varying the time of occurrence of leading edge, the trailing edge or both edges of the pulse in accordance with modulating wave. It is also called Pulse Duration Modulation.